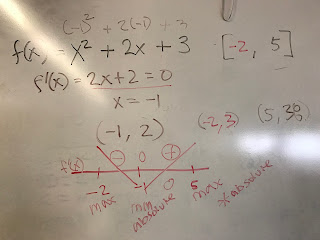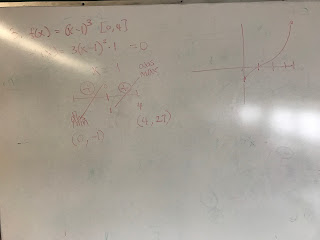1. Find the critical point and draw a number line with the critical point and the end points on it.
2. Find the slope around those points, which will tell you whether the point is a max or a min.
- for example, if the right end point has positive slope leading to it, then that would mean that the endpoint must be a maximum.
3. Find the y values (by plugging the x values into f(x)) for each max and min, then determine which is the absolute max and which is the absolute min. There has to be one of each, unless there is no maximum or minimum at all.
Functions:

Here are the problems we did in class that may help: